Vamos pensar nas ondas eletromagnéticas. Os fundamentos do eletromagnetismo estão elegantemente expressos nas equações de Maxwell. A partir delas, Maxwell deduziu a velocidade de propagação dessas ondas: Vamos pensar nas ondas eletromagnéticas. Os fundamentos do eletromagnetismo estão elegantemente expressos nas equações de Maxwell. A partir delas, Maxwell deduziu a velocidade de propagação dessas ondas:
Entretanto, as equações de Maxwell não são invariantes frente às transformações de Galileu. Uma maneira simples é pensar na velocidade relativa.
A partir das transformações de Galileu podemos obter as relações de transformação de velocidades e aceleração. Ou seja, relacionar a velocidade e a aceleração de um ponto vista dos dois referenciais inerciais. Para ser mais geral, podemos escrever para a velocidade:
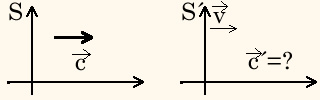
Assim, se um referencial inercial S mede a velocidade da luz como sendo c, qual é o valor medido por um referencial inercial S´ que se move com velocidade relativa em relação a S?
De acordo com as transformações de Galileu:
E se o sentido do movimento de S´for da direita para a esquerda:
Ou seja, o valor da velocidade da luz não é igual a c em todos os referenciais inerciais e mais, não é isotrópica!
|

 Vamos pensar nas ondas eletromagnéticas. Os fundamentos do eletromagnetismo estão elegantemente expressos nas equações de Maxwell. A partir delas, Maxwell deduziu a velocidade de propagação dessas ondas:
Vamos pensar nas ondas eletromagnéticas. Os fundamentos do eletromagnetismo estão elegantemente expressos nas equações de Maxwell. A partir delas, Maxwell deduziu a velocidade de propagação dessas ondas: