As novas regras
| Site: | Moodle UFSC - Apoio aos Cursos Presenciais |
| Curso: | Design Instrucional em Ambiente Virtual de Aprendizagem |
| Livro: | As novas regras |
| Impresso por: | Usuário visitante |
| Data: | terça-feira, 3 fev. 2026, 01:43 |
Descrição
.
 Vimos que o limite de velocidade máxima é a velocidade da luz c. Para altas velocidades, as transformações de Galileu levam a inconsistências, permitindo-se chegar a velocidades superiores à da luz. Sendo assim, quem dá as cartas agora são as transformações de Lorentz que nos levará a algo aparentemente estranho, mas que não viola o princípio da constância da velocidade da luz: c + c = c!   |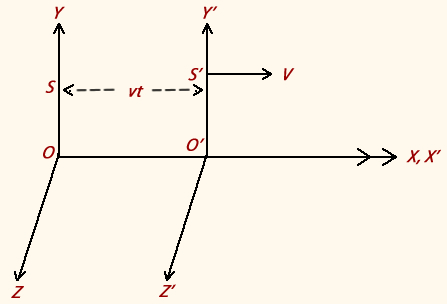
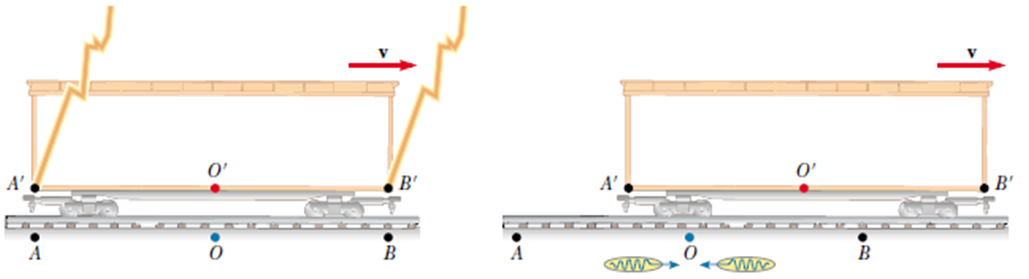
 A SIMULTANEIDADE É RELATIVA .......................................................................  Sendo assim, os dois observadores não concordam sobre a simultaneidade dos eventos. 
 |
 O TEMPO DILATA .......................................................................  De acordo com o que foi exibido no vídeo:
|
|
 COMPOSIÇÃO DE VELOCIDADES ........................................................................ Agora podemos compor velocidades de maneira a não infringir o segundo postulado, o da constância da velocidade da luz. Para isso, 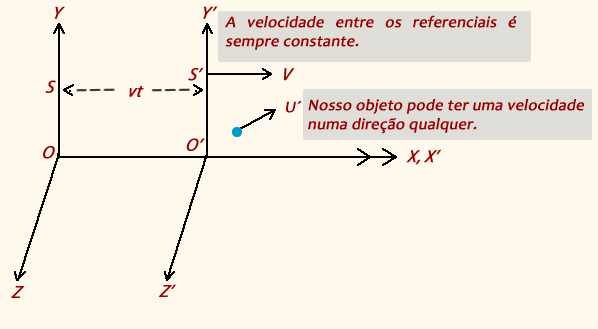  (1) A velocidade de um objeto não excede a velocidade da luz; (2) A velocidade da luz é igual em todas as direções. De acordo com as transformações de Galileu, um feixe de luz que viaja com velocidade c na direção X´, visto do referencial S, sua velocidade seria c+v! Veja que aqui, ela será igual a c. |
 Mudanças radicais I: massa relativística e momento linear ........................................................................................ Uma mudança radical acontece com a massa das partículas a altas velocidades. Nesse regime é preciso reformular o conceito de massa e considerar que a massa das partículas dependa de sua velocidade: 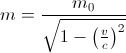 Onde: m0 é chamada “massa de repouso” da partícula porque se na expressão acima  Esse resultado surgiu bem antes da formulação da Relatividade Restrita cuja autoria normalmente é atribuída somente a Einstein em 1905. E foi confirmado experimentalmente em uma série de experimentos realizados entre 1901 e 1915. Por exemplo, os dados experimentais de um experimento feito por A.H. Bucherer em 1909, mostra o acordo com a equação da massa relativística (curva contínua): 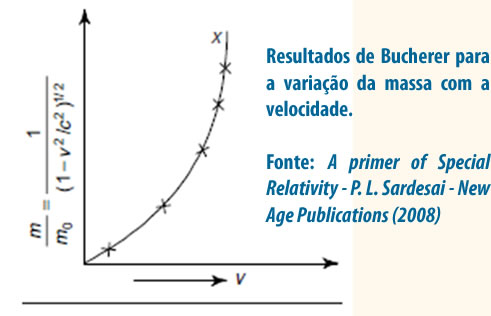  Logo, o momento conservado é o definido acima e não o conhecido por nós na mecânica newtoniana:  |
 MUDANÇAS RADICAIS II: relação entre massa e energia 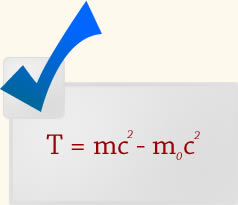............................................................................................  Na mecânica clássica massa e energia são conceitos distintos com propriedades físicas distintas. Já sabemos que o trabalho W realizado para acelerar uma partícula do repouso até uma velocidade v é igual ao aumento na energia cinética T da partícula (Teorema Trabalho-Energia Cinética). Na relatividade, ao efetuarmos esse cálculo chegamos a uma redefinição da energia cinética na relatividade que passa a ser definida como: 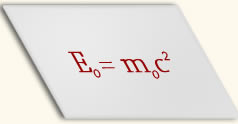 Essa relação relativística é cheia de novidades interessantíssimas e que causou uma revolução na Física e em áreas afins com as aplicações tecnológicas decorrentes. Primeira novidade: nessa expressão o segundo termo introduz uma energia que não tem análogo clássico e que depende somente da massa de repouso sendo constante. Essa energia é chamada energia de repouso da partícula. Assim, a cada massa de repouso m0 há uma energia de repouso que nos permite interpretar que a massa de repouso é mais uma forma de energia!A segunda novidade: o primeiro termo é entendido como sendo a energia total relativística da partícula.  O que leva à fusão dos conceitos de massa e energia numa única lei de conservação de massa-energia. Massa e energia são grandezas intercambiáveis na Relatividade Restrita. É importante perceber também que o trabalho realizado sobre a partícula leva a um aumento em sua massa: 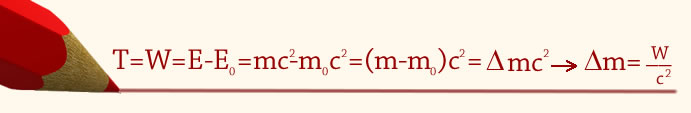 Perceba que se  a energia tende a um valor infinito. Ou seja, um trabalho infinito precisaria ser realizado para acelerar a partícula até uma velocidade igual a c. A velocidade da luz coloca então um limite de velocidade que não pode ser ultrapassado! |
 DINÂMICA RELATIVÍSTICA: partículas sem massa ..................................................................................................... A relatividade restrita possibilita também a obtenção da relação entre energia e momento de linear para partículas sem massa. Isso porque a energia total relativística também pode ser escrita como:
E2 = (pc)2 + (m0c2)2
 Se m0 = 0 -> E = pc. Esse é o caso, por exemplo, dos fotóns que possuem massa de repouso nula. Ou seja, eles viajam à velocidade da luz, o que impossibilita encontrar um referencial no qual o fóton esteja em repouso. |