Definições
| Site: | Moodle UFSC - Apoio aos Cursos Presenciais |
| Curso: | Design Instrucional em Ambiente Virtual de Aprendizagem |
| Livro: | Definições |
| Impresso por: | Usuário visitante |
| Data: | terça-feira, 3 fev. 2026, 02:06 |
Índice
- ONDAS MECÂNICAS
- O que é uma onda?
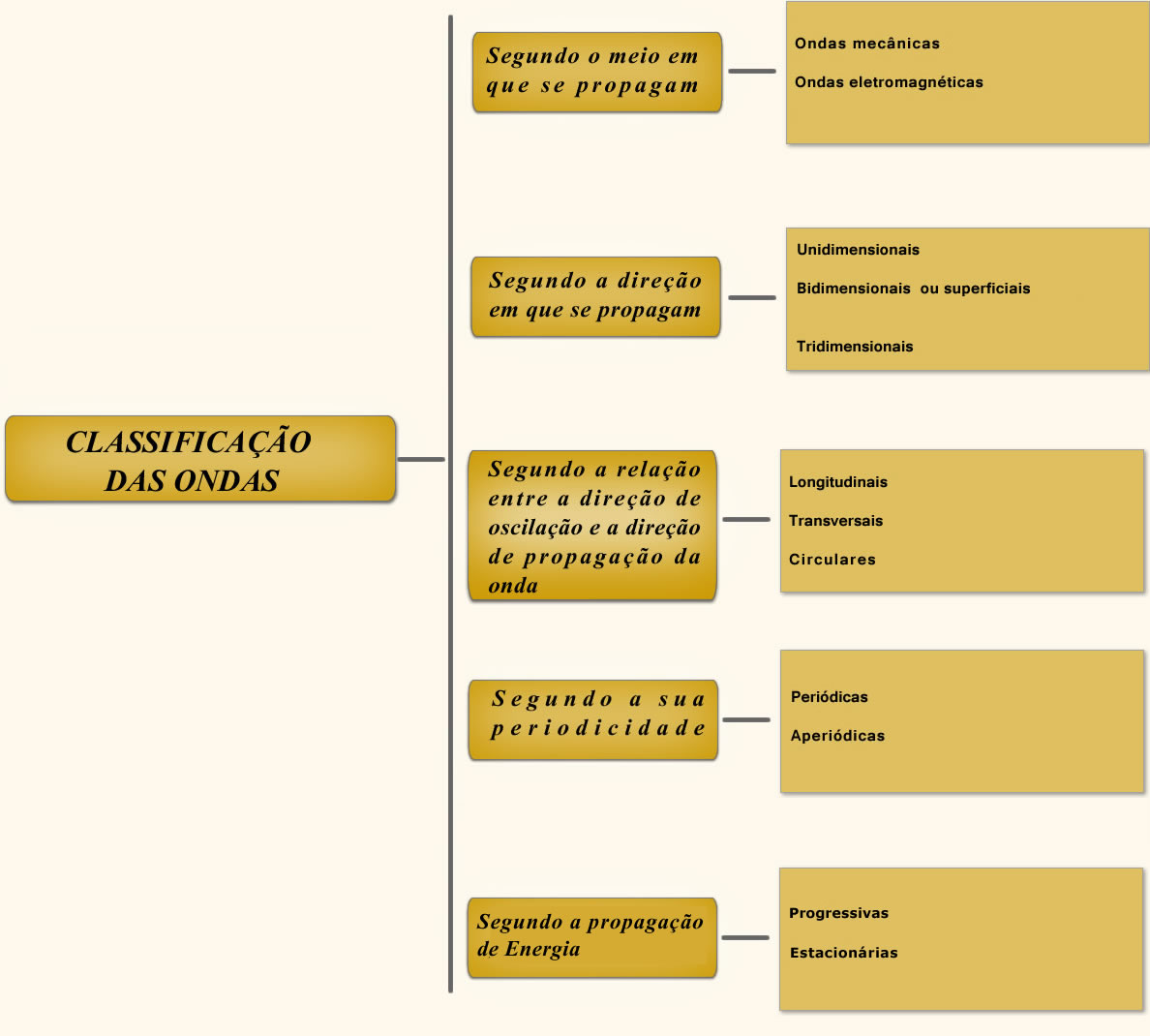
- Classificação das Ondas
- Segundo o meio em que se propagam:
- Segundo a direção em que se propagam:
- Ondas Unidimensionais
- Ondas Bidimensionais
- Ondas Tridimensonais
- Segundo a relação entre a direção de oscilação e a direção de propagação da onda:
- Ondas Transversais
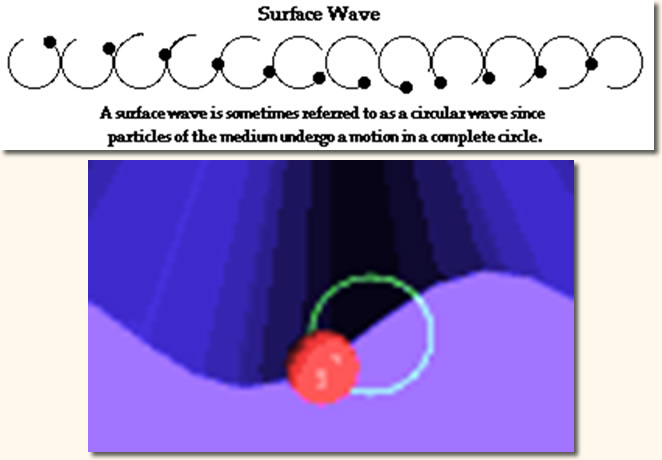
- Ondas Circulares
- Segundo a sua periodicidade
- Segundo a propagação de energia
- Ondas progressivas unidimensionais
- Grandezas características
- Ondas Harmônicas: gráficos
- Ondas Harmônicas: unidades no gráfico

|
Elas podem necessitar ou não de um meio de propagação. Para aquelas que necessitam de um meio de propagação ele pode ser de diversas naturezas: sólido, líquido ou gasoso. |
|
|
|
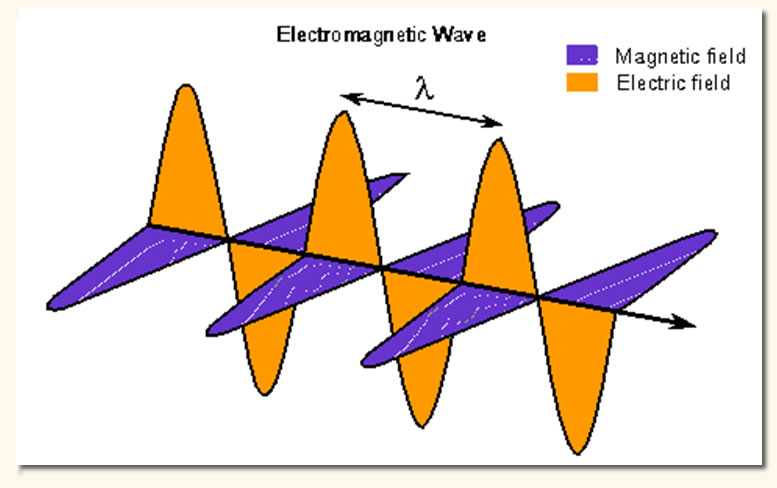
Ondas mecânicas: Ondas eletromagnéticas: |
|
As ondas podem ser classificadas de acordo com a direção de propagação: |
|
Ondas unidimensionais: 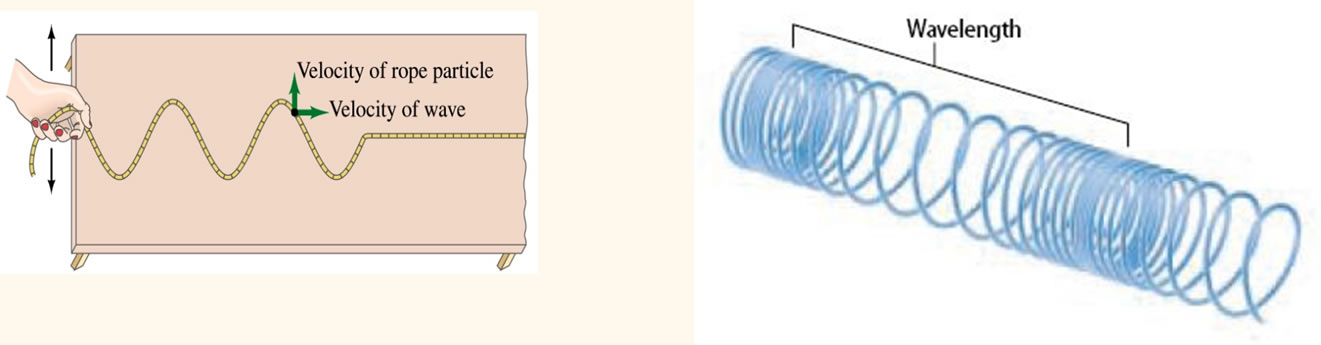 |
 São ondas que se propagam num plano. Um exemplo são as ondas que se produzem numa superfície líquida quando, por exemplo, se deixa cair uma pedra nela.   |

São ondas que se propagam no espaço tridimensional.
Exemplos:
Ondas Sonoras e Ondas de luz (Ondas Eletromagnéticas)
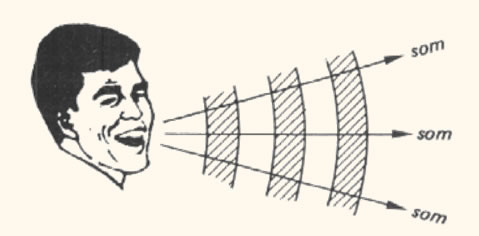

Para uma fonte pontual, por exemplo, de ondas sonoras, as ondas se movem em três direções sendo as frentes de onda superfícies esféricas concêntricas. O movimento de qualquer conjunto de frentes de onda pode ser representado por raios, os quais são linhas retas perpendiculares às frentes de onda como ilustrado na figura acima.
A grandes distâncias de uma fonte pontual, uma pequena parte de uma frente de onda pode ser aproximada por um plano, enquanto os raios são aproximadamente linhas paralelas. Chamamos essa aproximação de onda plana conforme ilustrado na figura abaixo:

A direção de oscilação de uma partícula do meio é paralela à direção de propagação da onda.


A direção de vibração das partículas do meio é perpendicular à direção de propagação da onda.
Exemplos:
- Ondas numa corda;
- Ondas numa mola;
- Ondas eletromagnéticas.

 |

Ondas periódicas
A perturbação se produz em ciclos repetitivos.
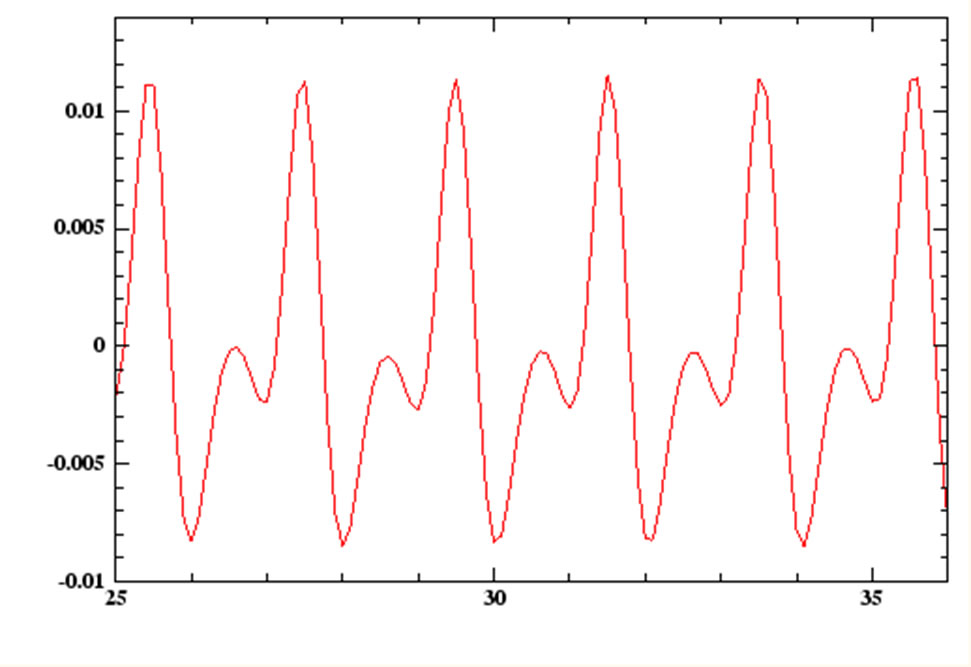
Ondas aperiódicas
A perturbação que as origina ocorre isoladamente ou, no caso que se repita, as perturbações sucessivas têm características diferentes.
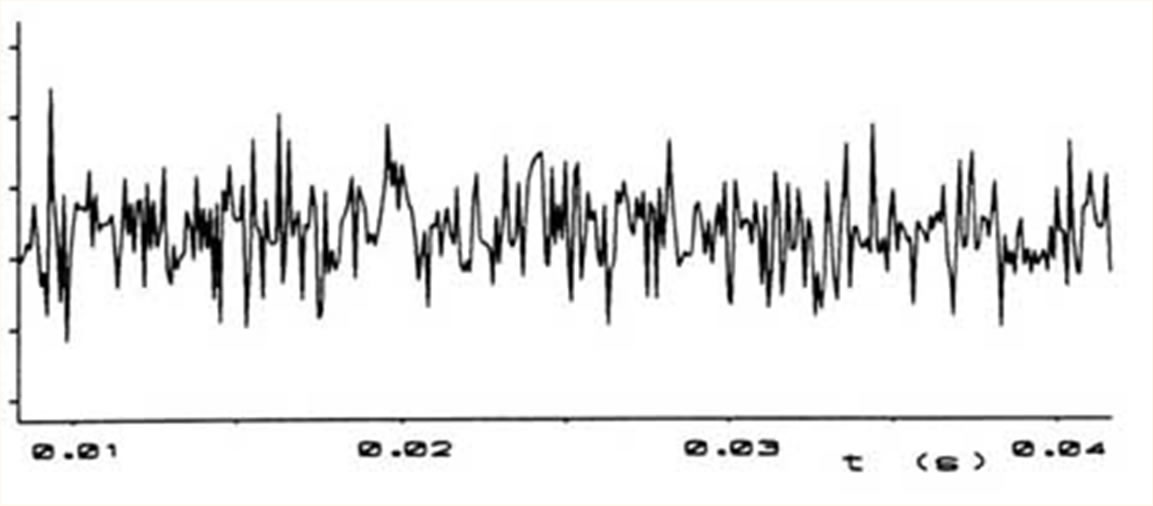

Ondas Progressivas
As ondas progressivas são aquelas em que a configuração da onda se move, observamos que há propagação de pulsos.
Nelas há transporte de energia e momento linear de um extremo de um ponto a outro do meio.
Ondas Estacionárias
As ondas estacionárias são aquelas em que a configuração da onda não se move, obeservamos que não há propagação de pulsos.
Nelas não há transporte de energia e de momento linear de um extremo ao outro do meio. Ou seja, a taxa média de transferência de energia é igual a zero em todos os pontos.
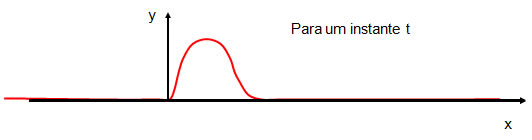
 Para realizar a descrição de uma onda vamos escolher uma classe simples delas que são as ondas progressivas em 1 dimensão. A ideia é obter a descrição matemática de um pulso que se propaga numa corda. 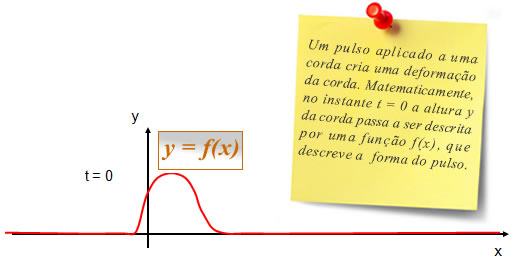 Com o passar do tempo, o pulso se move, mas mantém sua forma. 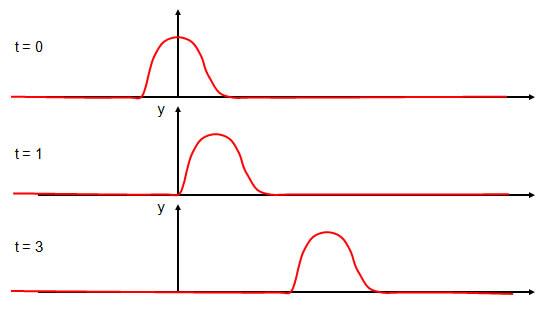 |
|
Descrição matemática Vamos considerar um pulso que se propaga numa corda esticada. A direção de deslocamento da partícula é a do eixo y e a direção de propagação do pulso é a do eixo x. Assim, queremos obter uma equação do tipo y(x,t):
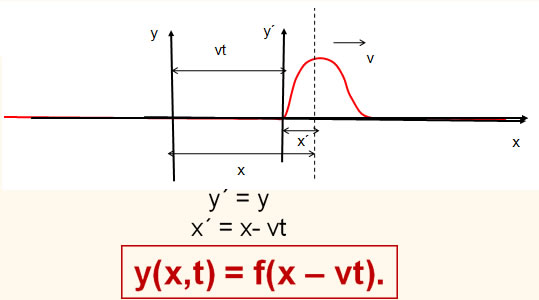 Interpretação: 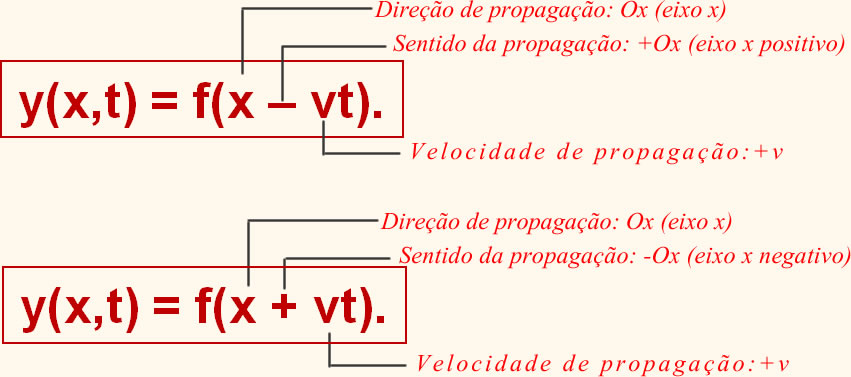 |
|
Mas, somente as ondas harmônicas são a única possibilidade à descrição de uma onda progressiva? |

Vamos descrever a seguir as grandezas características de um movimento periódico e que aparecem na função de onda senoidal:
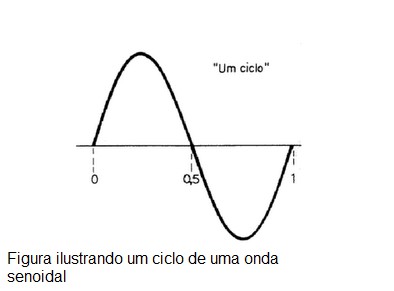

A amplitude corresponde ao valor do deslocamento máximo da onda:
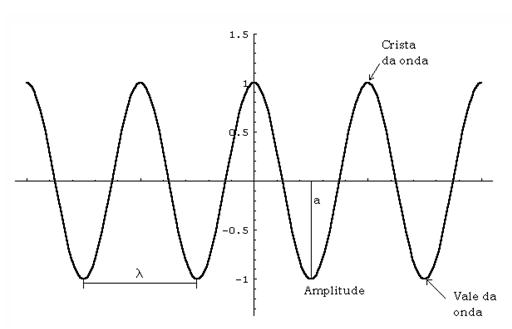

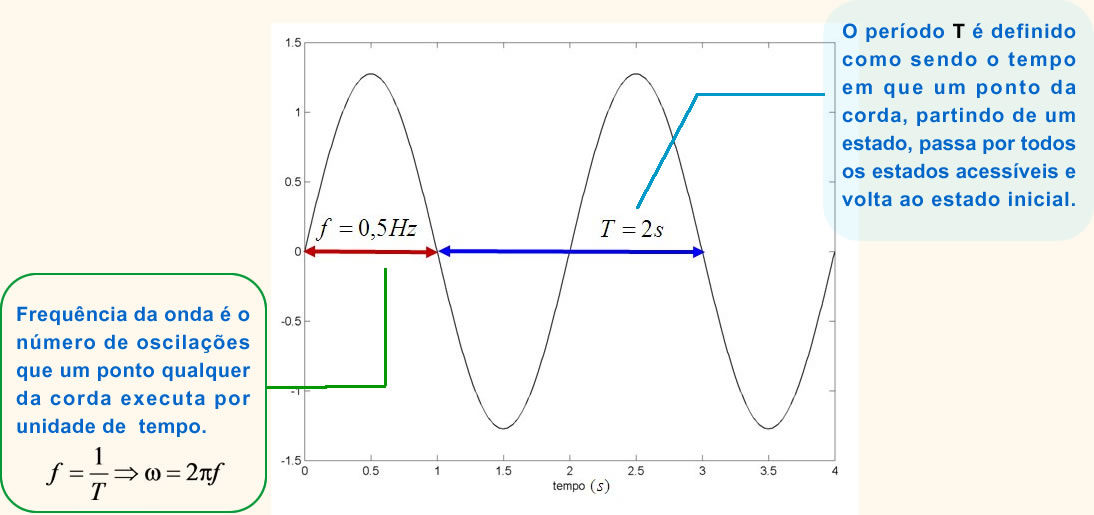

O comprimento de onda representa uma oscilação completa no espaço da posição. Ou seja, é a distãncia paralela à direção em que a onda se propaga entre repetições da forma da onda:
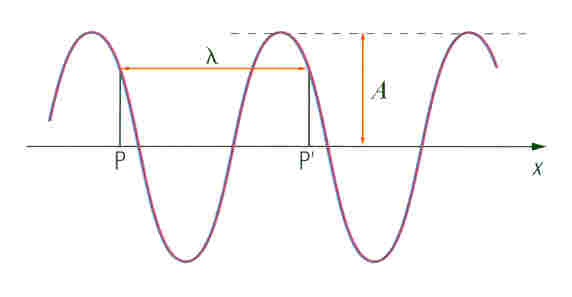
O número de onda k, representa uma contagem em unidade de comprimento de onda. É definido como:
![]()
Às vezes, o fator no numerador é omitido. Fique atento às definições utilizadas!
|
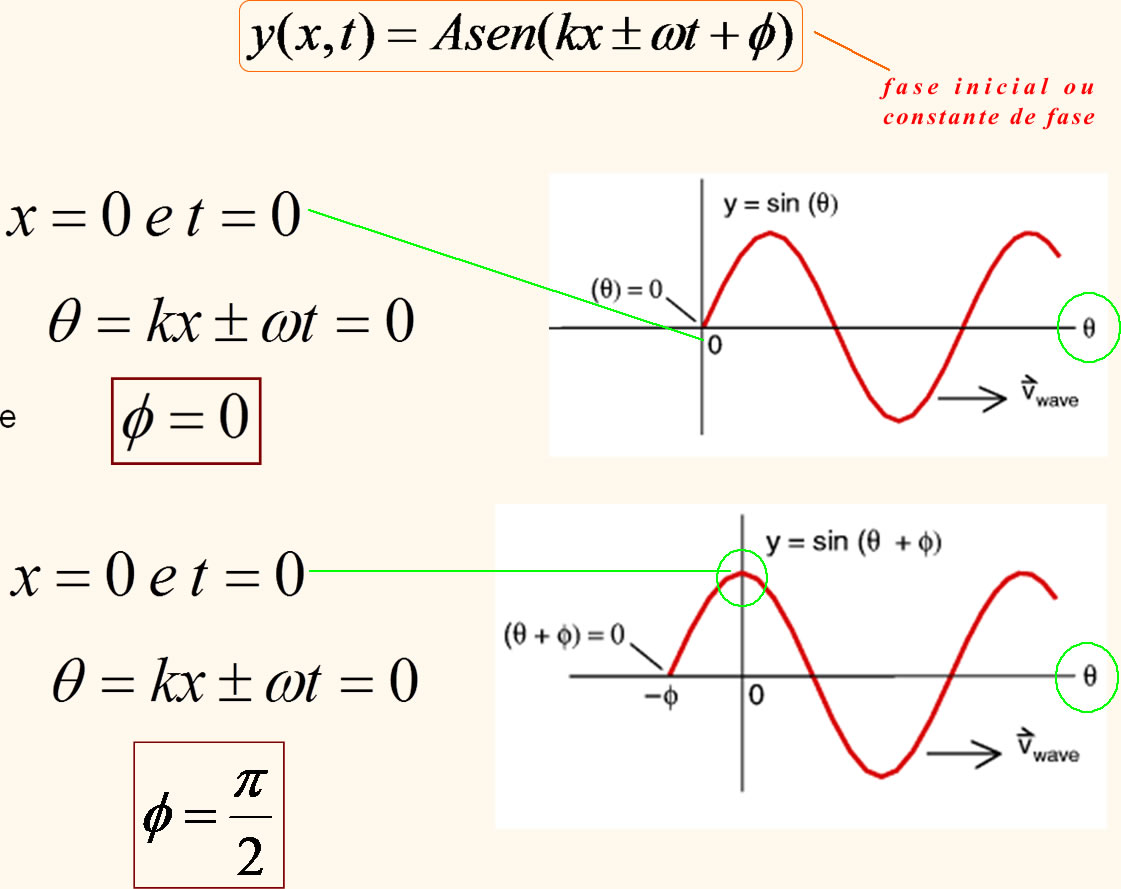
A fase inicial de uma onda fornece o valor do deslocamento e a inclinação da corda ao passar pela origem no instante t=0. Vejamos as duas situações abaixo. Na primeira o deslocamento é nulo e na segunda diferente de zero: |

Na prática uma onda senoidal pode ser criada numa corda a partir da execução de um movimento harmônico simples numa de suas extremidades. Para entender melhor o valor da fase inicial podemos fazer uma analogia entre o Movimento Harmônico Simples (MHS) e o Movimento Circular Uniforme (MCU):
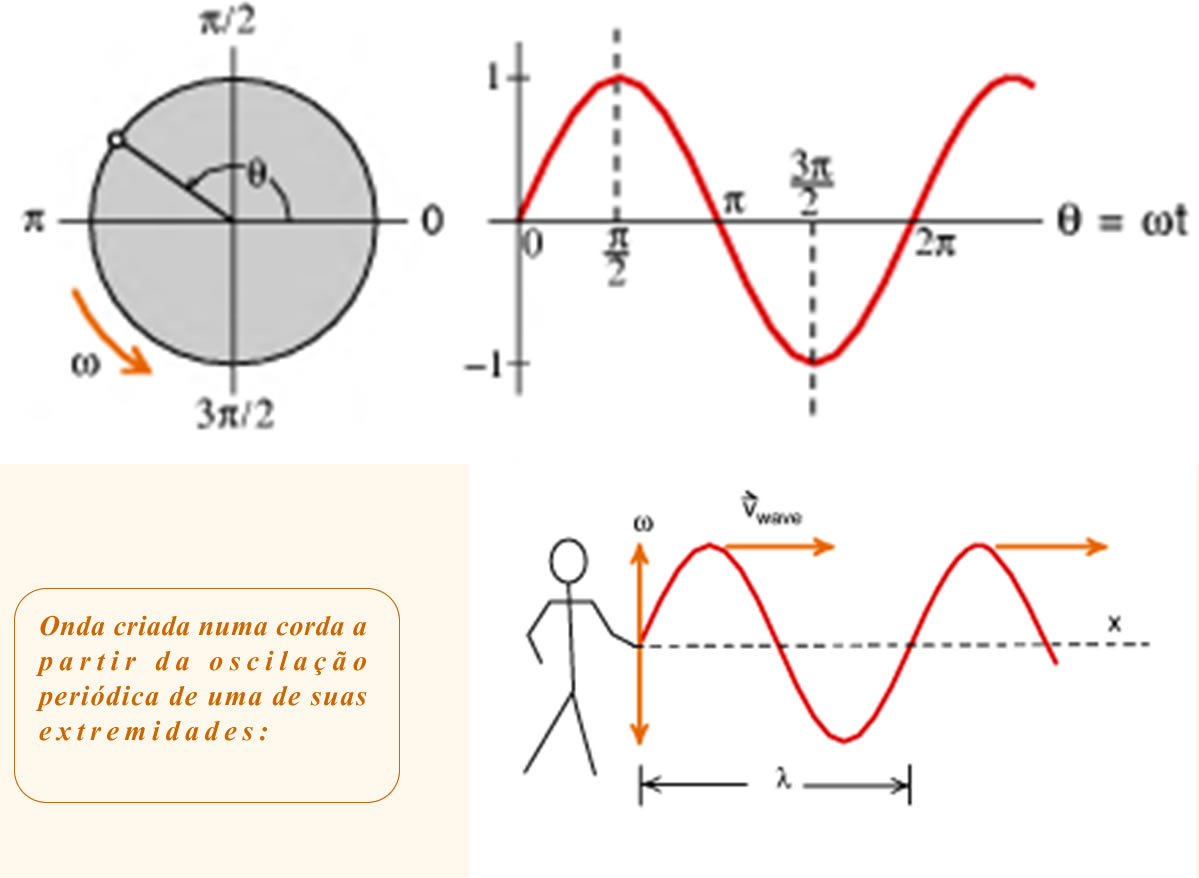 |

O gráfico abaixo nos ilustra ondas progressivas para t = 0 com diferentes valores para da fase inicial representando um deslocamento espacial entre elas.
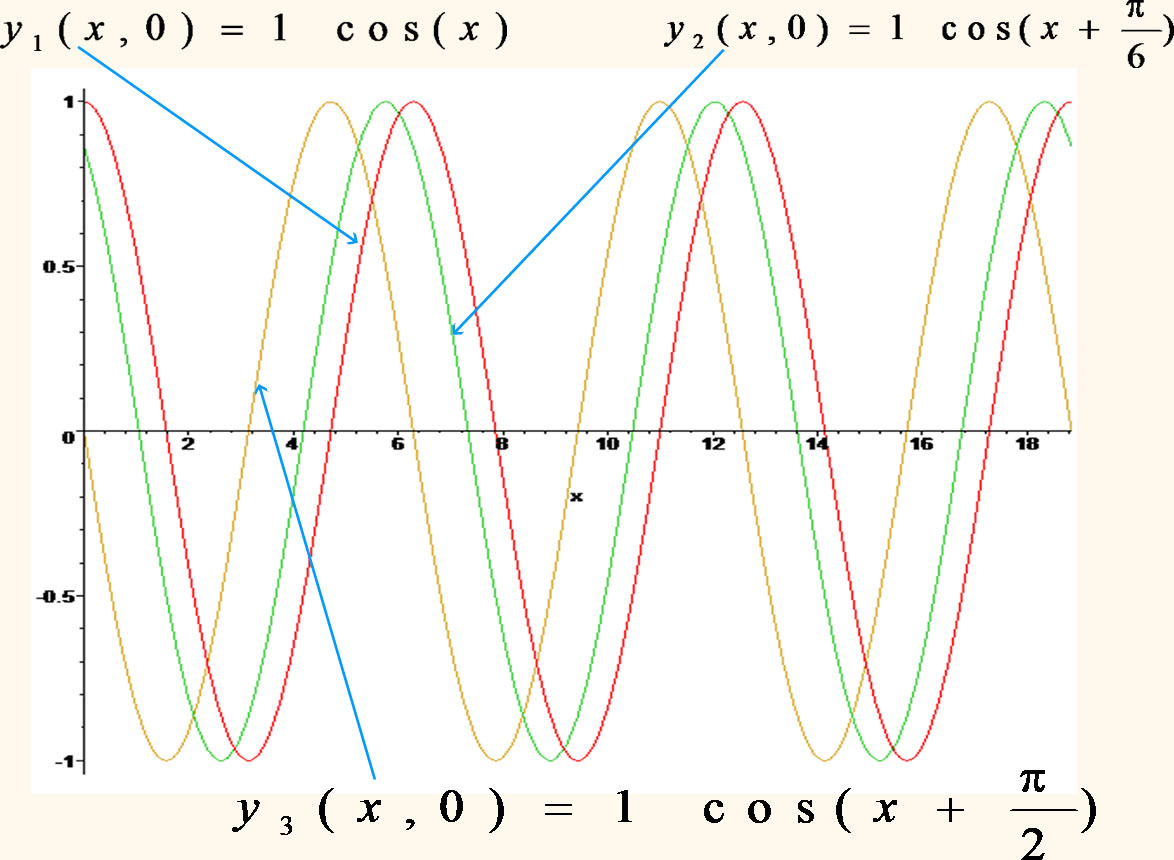
|
A onda se propaga com uma velocidade. Essa velocidade equivale àquela que você deveria caminhar para se manter ao lado de um pulso. Essa é a velocidade de propagação ou velocidade de fase. Para obtê-la vamos olhar para a fase da onda que é constante (um pulso se move com velocidade constante e sem mudar de forma): |

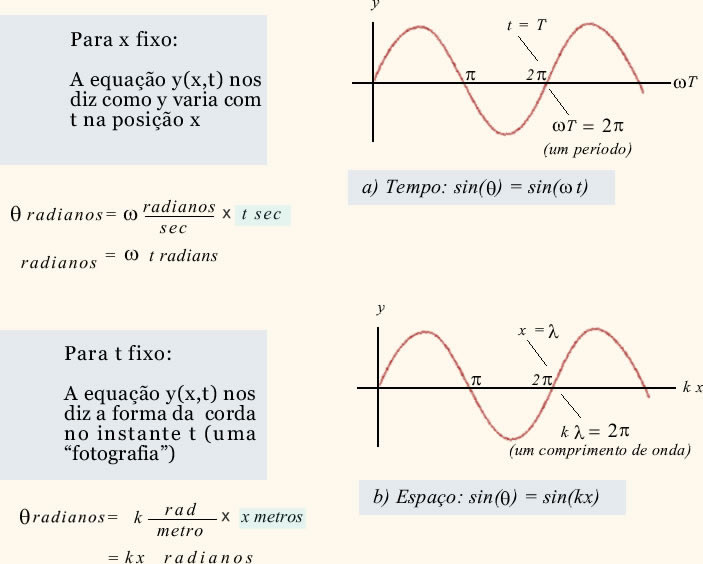
Representação Gráfica
Como a função de onda depende de dois parâmetros num gráfico bidimensional devemos fixar um deles e representar o deslocamento em função do outro parâmetro. Dessa forma temos:
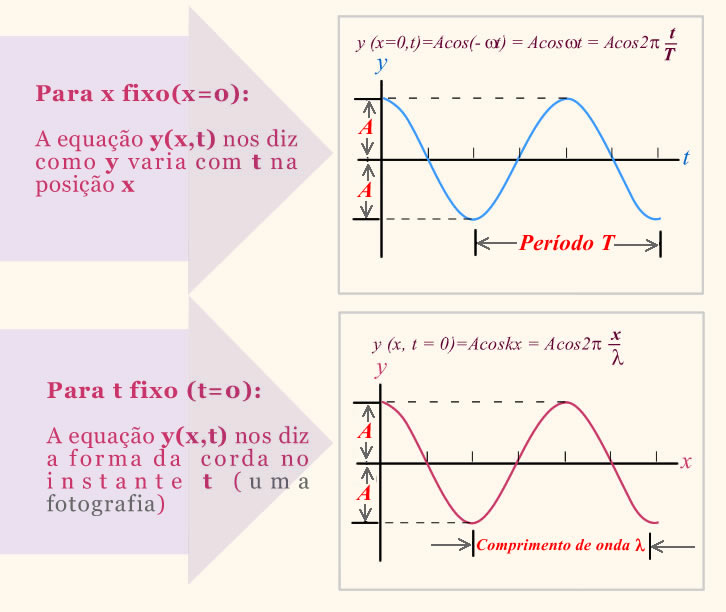

Ondas Harmônicas: unidades no gráfico