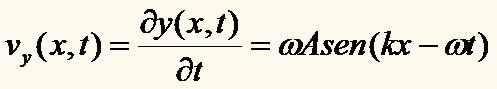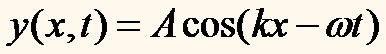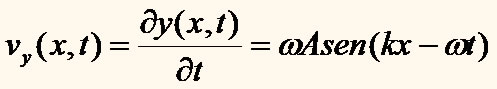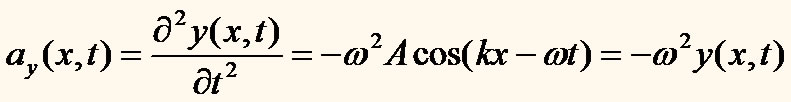Imprimir o livro todoImprimir o livro todo

Cinemática

Site: Moodle UFSC - Apoio aos Cursos Presenciais
Curso: Design Instrucional em Ambiente Virtual de Aprendizagem
Livro: Cinemática
Impresso por: Usuário visitante
Data: terça-feira, 3 fev. 2026, 02:00

Descrição

Notas de Aula III

Índice

Exatamente como na Mecânica que você estou em Física I, o objetivo da Cinemática é a descrição do movimento cujas grandezas relevantes são as  que descrevemos até aqui (velocidade de propagação, amplitude, frequência, comprimento de onda, número de onda, frequência angular) e as que vamos definir agora: posição, velocidade e aceleração de elementos individuais da corda.

Velocidade transversal de um elemento da corda

Uma função de onda que descreve uma onda senoidal progressiva na direção positiva do eixo x numa corda é:


                                        y(x,t) = A cos(kx - ωt)

 A velocidade transversal é obtida a partir da taxa de variação do deslocamento no tempo:
                                                    .

A representação gráfica em função do tempo para x= 0 é:




A função de onda que descreve uma onda senoidal progressiva na direção positiva do eixo x numa corda é:
                                                     .

 Taxa de variação do deslocamento no tempo:


                                                     .

 A aceleração transversal de um elemento da corda é a taxa de variação da
velocidade transversal no tempo:


                                                  .

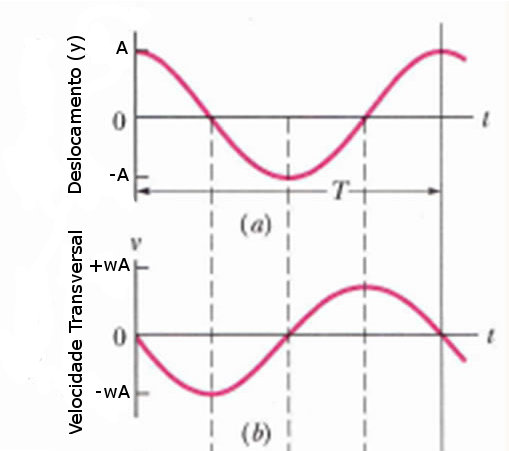
A representação gráfica em função do tempo para x=0 é:


 

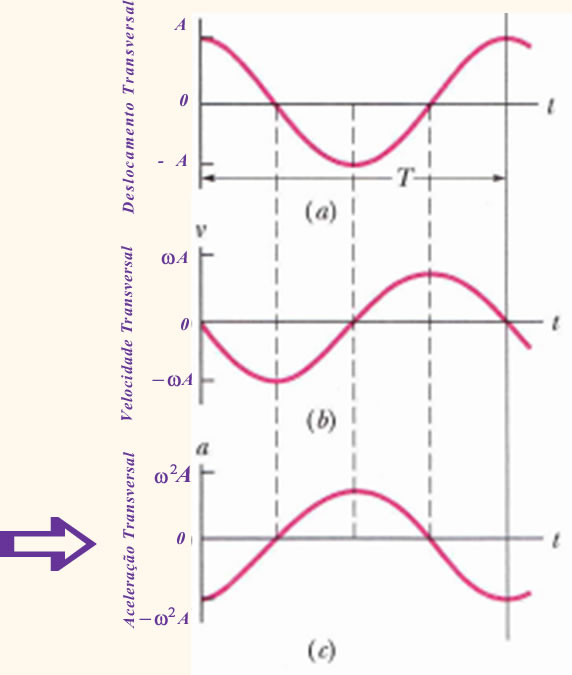
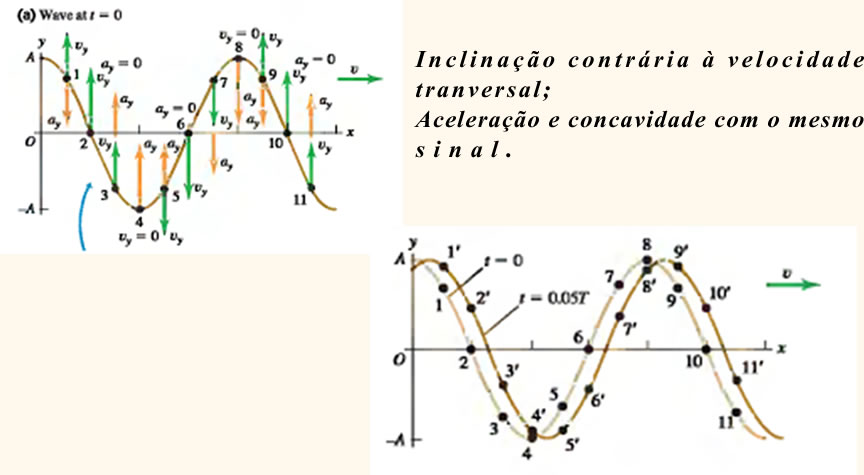
Como relacionar a velocidade transversal e a aceleração transversal com a inclinação e a concavidade?


Vamos olhar para a parte espacial da função de onda:


.

Agora vamos combinar tudo, ou seja, tanto a parte espacial quanto a parte temporal da função de onda:


.


Visualizando tudo num único gráfico, o do deslocamento em função da posição temos:

,





A função de onda é uma função que é solução da equação de onda. A equação de onda é equivalente à segunda lei de Newton. E as funções de onda possíveis são aquelas que satisfazem à equação de onda definida em 1d como:

ç

A velocidade de propagação da onda foi apresentada até agora utilizando-se a definição de velocidade de ondas periódicas:

                         v = λf      

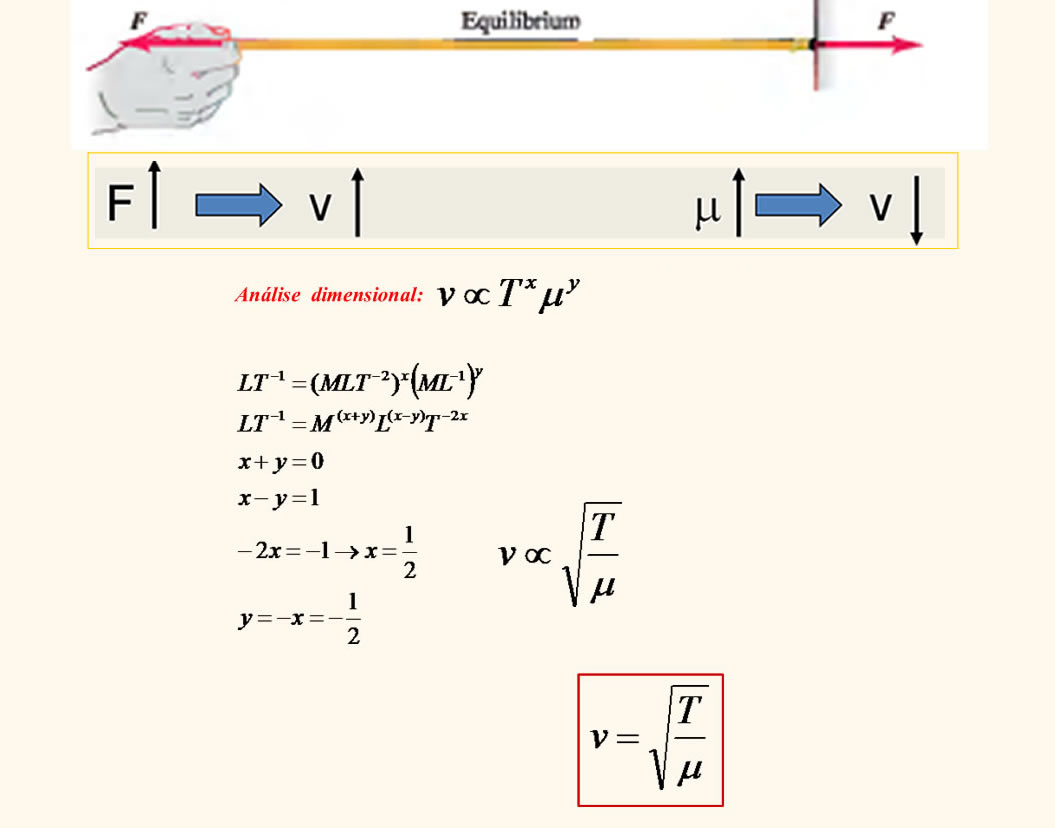
Entretanto, podemos nos perguntar se essa velocidade pode ser obtida a partir de propriedades do meio.

Ela aumenta ou diminui com a tensão?

Ela aumenta ou diminui de acordo com a densidade linear de massa?

Há diferentes formas de se fazer essa dedução e apresentaremos duas delas a seguir.

Na primeira dedução vamos chegar à velocidade de fase a partir da análise dimensional:

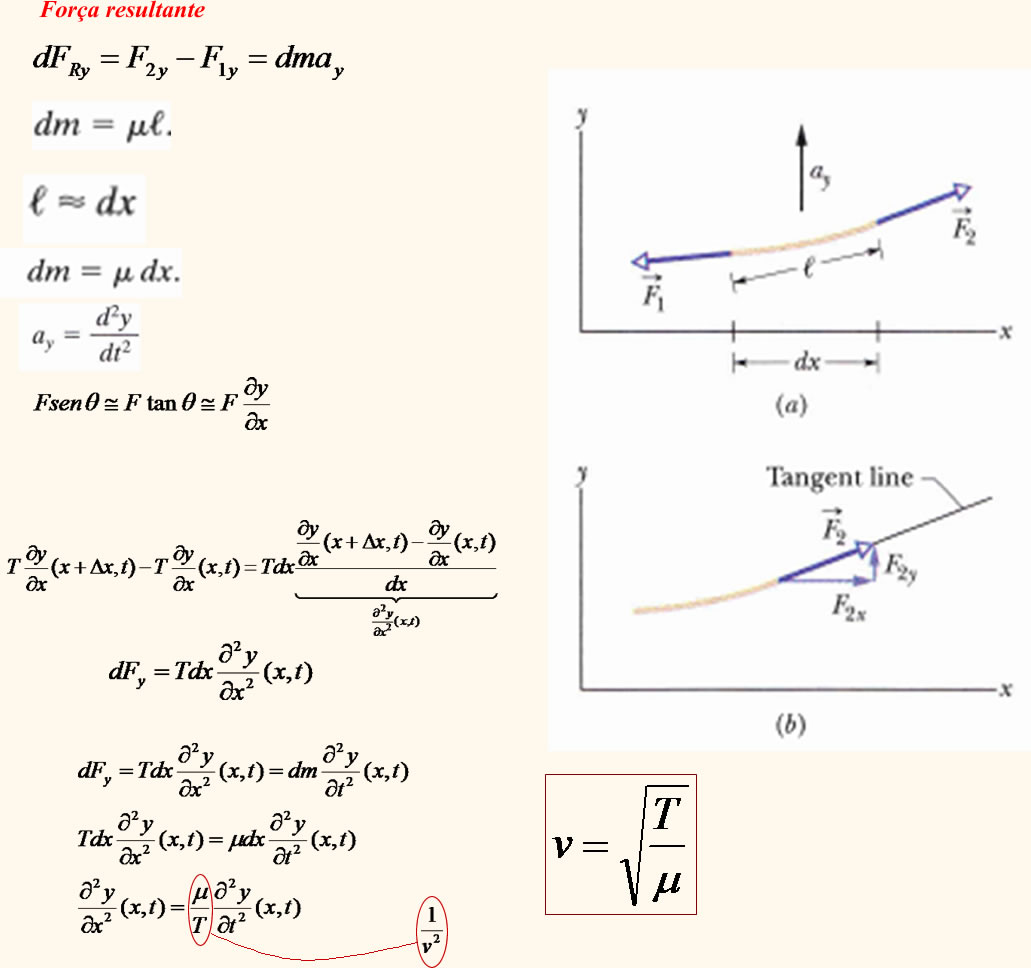
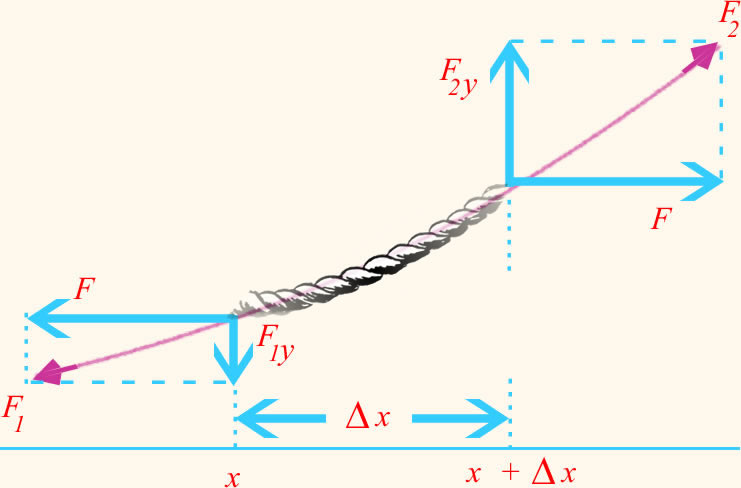
No segundo procedimento, vamos chegar à velocidade utilizando-se a segunda lei de Newton. Para isso, precisamos determinar qual é a força resultante responsável pelo movimento vertical de um elemento da corda. Olhando para um elemento da corda:

.